Utility Functions¶
Overview¶
This module provides various utility functions for radiometry calculations. Functions are provided for a maximally flat spectral filter, a simple photon detector spectral response, effective value calculation, conversion of spectral domain variables between [um], [cm^-1] and [Hz], conversion of spectral density quantities between [um], [cm^-1] and [Hz] and spectral convolution.
See the __main__ function for examples of use.
This package was partly developed to provide additional material in support of students and readers of the book Electro-Optical System Analysis and Design: A Radiometry Perspective, Cornelius J. Willers, ISBN 9780819495693, SPIE Monograph Volume PM236, SPIE Press, 2013. http://spie.org/x648.html?product_id=2021423&origin_id=x646
Module classes¶
-
class
pyradi.ryutils.Spectral(ID, value, wl=None, wn=None, desc=None)¶ Generic spectral can be used for any spectral vector
-
plot(filename=None, heading=None, ytitle='')¶ Do a simple plot of spectral variable(s)
- Args:
- filename (str): filename for png graphicheading (str): graph headingytitle (str): graph y-axis title
- Returns:
- Nothing, writes png file to disk
- Raises:
- No exception is raised.
-
vecalign(other)¶ returns two spectral values properly interpolated and aligned to same base
it is not intended that the function will be called directly by the user
- Args:
- other (Spectral): the other Spectral to be used in addition
- Returns:
- wl, wn, s, o
- Raises:
- No exception is raised.
-
-
class
pyradi.ryutils.Atmo(ID, distance=None, wl=None, wn=None, tran=None, atco=None, prad=None, desc=None)¶ Atmospheric spectral such as transittance or attenuation coefficient
-
pathR(distance)¶ Calculates the path radiance at distance
Distance is in m
- Args:
- distance (scalar or np.array (M,)): distance in m if transmittance, or None if att coeff
- Returns:
- transmittance (np.array (N,M) ): transmittance along N at distance along M
- Raises:
- No exception is raised.
-
tauR(distance)¶ Calculates the transmittance at distance
Distance is in m
- Args:
- distance (scalar or np.array (M,)): distance in m if transmittance, or None if att coeff
- Returns:
- transmittance (np.array (N,M) ): transmittance along N at distance along M
- Raises:
- No exception is raised.
-
-
class
pyradi.ryutils.Sensor(ID, fno, detarea, inttime, tauOpt=1, quantEff=1, pfrac=1, desc='')¶ Sensor characteristics
-
QE()¶ Returns scaler or np.array for detector quantEff
- Args:
- None
- Returns:
- str
- Raises:
- No exception is raised.
-
tauOpt()¶ Returns scaler or np.array for optics transmittance
- Args:
- None
- Returns:
- str
- Raises:
- No exception is raised.
-
-
class
pyradi.ryutils.Target(ID, tmprt, emis, refl=1, cosTarg=1, taumed=1, scale=1, desc='')¶ Target / Source characteristics
-
emis()¶ Returns scaler or np.array for emissivity
- Args:
- None
- Returns:
- str
- Raises:
- No exception is raised.
-
radiance(units='el')¶ Returns radiance spectral for target
- The type of spectral is one of the following:
type=’el [W/(m$^2$.$mu$m)] type=’ql’ [q/(s.m$^2$.$mu$m)] type=’en’ [W/(m$^2$.cm$^{-1}$)] type=’qn’ [q/(s.m$^2$.cm$^{-1}$)]
- Args:
- None
- Returns:
- str
- Raises:
- No exception is raised.
-
refl()¶ Returns scaler or np.array for reflectance
- Args:
- None
- Returns:
- str
- Raises:
- No exception is raised.
-
taumed()¶ Returns scaler or np.array for atmospheric transmittance to illuminating source
- Args:
- None
- Returns:
- str
- Raises:
- No exception is raised.
-
Module functions¶
-
pyradi.ryutils.sfilter(spectral, center, width, exponent=6, taupass=1.0, taustop=0.0, filtertype='bandpass')¶ Calculate a symmetrical filter response of shape exp(-x^n)
Given a number of parameters, calculates maximally flat, symmetrical transmittance. The function parameters controls the width, pass-band and stop-band transmittance and sharpness of cutoff. This function is not meant to replace the use of properly measured filter responses, but rather serves as a starting point if no other information is available. This function does not calculate ripple in the pass-band or cut-off band.
Filter types supported include band pass, high (long) pass and low (short) pass filters. High pass filters have maximal transmittance for all spectral values higher than the central value. Low pass filters have maximal transmittance for all spectral values lower than the central value.
- Args:
- spectral (np.array[N,] or [N,1]): spectral vector in [um] or [cm-1].center (float): central value for filter passbandwidth (float): proportional to width of filter passbandexponent (float): even integer, define the sharpness of cutoff.If exponent=2 then gaussianIf exponent=infinity then squaretaupass (float): the transmittance in the pass band (assumed constant)taustop (float): peak transmittance in the stop band (assumed constant)filtertype (string): filter type, one of ‘bandpass’, ‘lowpass’ or ‘highpass’
- Returns:
- transmittance (np.array[N,] or [N,1]): transmittances at “spectral” intervals.
- Raises:
- No exception is raised.If an invalid filter type is specified, return None.If negative spectral is specified, return None.
-
pyradi.ryutils.responsivity(wavelength, lwavepeak, cuton=1, cutoff=20, scaling=1.0)¶ Calculate a photon detector wavelength spectral responsivity
Given a number of parameters, calculates a shape that is somewhat similar to a photon detector spectral response, on wavelength scale. The function parameters controls the cutoff wavelength and shape of the response. This function is not meant to replace the use of properly measured spectral responses, but rather serves as a starting point if no other information is available.
- Args:
- wavelength (np.array[N,] or [N,1]): vector in [um].lwavepeak (float): approximate wavelength at peak responsecutoff (float): cutoff strength beyond peak, 5 < cutoff < 50cuton (float): cuton sharpness below peak, 0.5 < cuton < 5scaling (float): scaling factor
- Returns:
- responsivity (np.array[N,] or [N,1]): responsivity at wavelength intervals.
- Raises:
- No exception is raised.
-
pyradi.ryutils.effectiveValue(spectraldomain, spectralToProcess, spectralBaseline)¶ Normalise a spectral quantity to a scalar, using a weighted mapping by another spectral quantity.
Effectivevalue = integral(spectralToProcess * spectralBaseline) / integral( spectralBaseline)
The data in spectralToProcess and spectralBaseline must both be sampled at the same domain values as specified in spectraldomain.
The integral is calculated with numpy/scipy trapz trapezoidal integration function.
- Args:
- inspectraldomain (np.array[N,] or [N,1]): spectral domain in wavelength, frequency or wavenumber.spectralToProcess (np.array[N,] or [N,1]): spectral quantity to be normalisedspectralBaseline (np.array[N,] or [N,1]): spectral serving as baseline for normalisation
- Returns:
- (float): effective valueReturns None if there is a problem
- Raises:
- No exception is raised.
-
pyradi.ryutils.convertSpectralDomain(inspectraldomain, type='')¶ Convert spectral domains, i.e. between wavelength [um], wavenummber [cm^-1] and frequency [Hz]
In string variable type, the ‘from’ domain and ‘to’ domains are indicated each with a single letter: ‘f’ for temporal frequency, ‘l’ for wavelength and ‘n’ for wavenumber The ‘from’ domain is the first letter and the ‘to’ domain the second letter.
Note that the ‘to’ domain vector is a direct conversion of the ‘from’ domain to the ‘to’ domain (not interpolated or otherwise sampled.
- Args:
- inspectraldomain (np.array[N,] or [N,1]): spectral domain in wavelength, frequency or wavenumber.wavelength vector in [um]frequency vector in [Hz]wavenumber vector in [cm^-1]type (string): specify from and to domains:‘lf’ convert from wavelength to per frequency‘ln’ convert from wavelength to per wavenumber‘fl’ convert from frequency to per wavelength‘fn’ convert from frequency to per wavenumber‘nl’ convert from wavenumber to per wavelength‘nf’ convert from wavenumber to per frequency
- Returns:
- [N,1]: outspectraldomainReturns zero length array if type is illegal, i.e. not one of the expected values
- Raises:
- No exception is raised.
-
pyradi.ryutils.convertSpectralDensity(inspectraldomain, inspectralquantity, type='')¶ Convert spectral density quantities, i.e. between W/(m^2.um), W/(m^2.cm^-1) and W/(m^2.Hz).
In string variable type, the ‘from’ domain and ‘to’ domains are indicated each with a single letter: ‘f’ for temporal frequency, ‘w’ for wavelength and ‘’n’ for wavenumber The ‘from’ domain is the first letter and the ‘to’ domain the second letter.
The return values from this function are always positive, i.e. not mathematically correct, but positive in the sense of radiance density.
The spectral density quantity input is given as a two vectors: the domain value vector and the density quantity vector. The output of the function is also two vectors, i.e. the ‘to’ domain value vector and the ‘to’ spectral density. Note that the ‘to’ domain vector is a direct conversion of the ‘from’ domain to the ‘to’ domain (not interpolated or otherwise sampled).
- Args:
- inspectraldomain (np.array[N,] or [N,1]): spectral domain in wavelength, frequency or wavenumber.inspectralquantity (np.array[N,] or [N,1]): spectral density in same domain as domain vector above.wavelength vector in [um]frequency vector in [Hz]wavenumber vector in [cm^-1]type (string): specify from and to domains:‘lf’ convert from per wavelength interval density to per frequency interval density‘ln’ convert from per wavelength interval density to per wavenumber interval density‘fl’ convert from per frequency interval density to per wavelength interval density‘fn’ convert from per frequency interval density to per wavenumber interval density‘nl’ convert from per wavenumber interval density to per wavelength interval density‘nf’ convert from per wavenumber interval density to per frequency interval density
- Returns:
- ([N,1],[N,1]): outspectraldomain and outspectralquantityReturns zero length arrays is type is illegal, i.e. not one of the expected values
- Raises:
- No exception is raised.
-
pyradi.ryutils.convolve(inspectral, samplingresolution, inwinwidth, outwinwidth, windowtype=<function bartlett>)¶ Convolve (non-circular) a spectral variable with a window function, given the input resolution and input and output window widths.
This function is normally used on wavenumber-domain spectral data. The spectral data is assumed sampled at samplingresolution wavenumber intervals. The inwinwidth and outwinwidth window function widths are full width half-max (FWHM) for the window functions for the inspectral and returned spectral variables, respectively. The Bartlett function is used as default, but the user can use a different function. The Bartlett function is a triangular function reaching zero at the ends. Window function width is correct for Bartlett and only approximate for other window functions.
Spectral convolution is best done in frequency domain ([cm-1] units) because the filter or emission line shapes have better symmetry in frequency domain than in wavelength domain.
The input spectral vector must be in spectral density units of cm-1.
- Args:
- inspectral (np.array[N,] or [N,1]): spectral variable input vector (e.g., radiance or transmittance).samplingresolution (float): wavenumber interval between inspectral samplesinwinwidth (float): FWHM window width used to obtain the input spectral vector (e.g., spectroradiometer window width)outwinwidth (float): FWHM window width of the output spectral vector after convolutionwindowtype (function): name of a numpy/scipy function for the window function
- Returns:
- outspectral (np.array[N,]): input vector, filtered to new window width.windowfn (np.array[N,]): The window function used.
- Raises:
- No exception is raised.
-
pyradi.ryutils.savitzkyGolay1D(y, window_size, order, deriv=0, rate=1)¶ Smooth (and optionally differentiate) data with a Savitzky-Golay filter.
Source: http://wiki.scipy.org/Cookbook/SavitzkyGolay
The Savitzky Golay filter is a particular type of low-pass filter, well adapted for data smoothing. For further information see: http://www.wire.tu-bs.de/OLDWEB/mameyer/cmr/savgol.pdf
The Savitzky-Golay filter removes high frequency noise from data. It has the advantage of preserving the original shape and features of the signal better than other types of filtering approaches, such as moving averages techniques.
The Savitzky-Golay is a type of low-pass filter, particularly suited for smoothing noisy data. The main idea behind this approach is to make for each point a least-square fit with a polynomial of high order over a odd-sized window centered at the point.
- Examples:
- t = np.linspace(-4, 4, 500) y = np.exp( -t**2 ) + np.random.normal(0, 0.05, t.shape) ysg = savitzky_golay(y, window_size=31, order=4) import matplotlib.pyplot as plt plt.plot(t, y, label=’Noisy signal’) plt.plot(t, np.exp(-t**2), ‘k’, lw=1.5, label=’Original signal’) plt.plot(t, ysg, ‘r’, label=’Filtered signal’) plt.legend() plt.show()
- References:
- [1] A. Savitzky, M. J. E. Golay, Smoothing and Differentiation of
- Data by Simplified Least Squares Procedures. Analytical Chemistry, 1964, 36 (8), pp 1627-1639.
- [2] Numerical Recipes 3rd Edition: The Art of Scientific Computing
- W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery Cambridge University Press ISBN-13: 9780521880688
- Args:
- y : array_like, shape (N,) the values of the time history of the signal.window_size : int the length of the window. Must be an odd integer number.order : int the order of the polynomial used in the filtering. Must be less then window_size - 1.deriv: int the order of the derivative to compute (default = 0 means only smoothing)
- Returns:
- ys : ndarray, shape (N) the smoothed signal (or it’s n-th derivative).
- Raises:
- Exception raised for window size errors.
-
pyradi.ryutils.abshumidity(T, equationSelect=1)¶ Atmopsheric absolute humidity [g/m3] for temperature in [K] between 248 K and 342 K.
This function provides two similar equations, but with different constants.
- Args:
- temperature (np.array[N,] or [N,1]): in [K].equationSelect (int): select the equation to be used.
- Returns:
- absolute humidity (np.array[N,] or [N,1]): abs humidity in [g/m3]
- Raises:
- No exception is raised.
-
pyradi.ryutils.rangeEquation(Intensity, Irradiance, rangeTab, tauTab, rangeGuess=1, n=2)¶ Solve the range equation for arbitrary transmittance vs range.
This function solve for the range
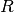 in the range equation
in the range equation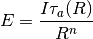
where
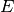 is the threshold irradiance in [W/m2],
and
is the threshold irradiance in [W/m2],
and 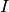 is the intensity in [W/sr]. This range equation holds for
the case where the target is smaller than the field of view.
is the intensity in [W/sr]. This range equation holds for
the case where the target is smaller than the field of view.The range
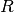 must be in [m], and
must be in [m], and 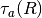 is calculated from a lookup table of atmospheric transmittance vs. range.
The transmittance lookup table can be calculated from the simple Bouguer law,
or it can have any arbitrary shape, provided it decreases with increasing range.
The user supplies the lookup table in the form of an array of range values and
an associated array of transmittance values. The range values need not be on
constant linear range increment.
is calculated from a lookup table of atmospheric transmittance vs. range.
The transmittance lookup table can be calculated from the simple Bouguer law,
or it can have any arbitrary shape, provided it decreases with increasing range.
The user supplies the lookup table in the form of an array of range values and
an associated array of transmittance values. The range values need not be on
constant linear range increment.The parameter
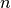
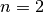 (default value) the general case of a radiating source
smaller than the field of view.
(default value) the general case of a radiating source
smaller than the field of view.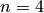 the special case of a laser range finder illuminating a target
smaller than the field of view, viewed against the sky. In this case there
is an
the special case of a laser range finder illuminating a target
smaller than the field of view, viewed against the sky. In this case there
is an 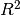 attenuation from the laser to the source and another
attenuation from the laser to the source and another
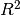 attenuation from the source to the receiver, hence
attenuation from the source to the receiver, hence
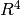 overall.
overall.
If the range solution is doubtful (e.g. not a trustworthy solution) the returned value is made negative.
- Args:
- Intensity (float or np.array[N,] or [N,1]): in [W/sr].Irradiance (float or np.array[N,] or [N,1]): in [W/m2].rangeTab (np.array[N,] or [N,1]): range vector for tauTab lookup in [m]tauTab (np.array[N,] or [N,1]): transmittance vector for lookup in [m]rangeGuess (float): starting value range estimate in [m] (optional)n (float): range power (2 or 4) (optional)
- Returns:
- range (float or np.array[N,] or [N,1]): Solution to the range equation in [m]. Value is negative if calculated range exceeds the top value in range table, or if calculated range is too near the lower resolution limit.
- Raises:
- No exception is raised.
-
pyradi.ryutils._rangeEquationCalc(r, i, e, tauTable, n, rMax)¶
-
pyradi.ryutils.detectThresholdToNoiseTpFAR(pulseWidth, FAR)¶ Solve for threshold to noise ratio, given pulse width and FAR, for matched filter.
Using the theory of matched filter design, calculate the threshold to noise ratio, to achieve a required false alarm rate.
References:
“Electro-optics handbook,” Tech. Rep. EOH-11, RCA, 1974. RCA Technical Series Publication.
- Hippenstiel, Detection Theory: Applications and Digital Signal Pro-cessing, CRC Press, 2002
- Args:
- pulseWidth (float): the signal pulse width in [s].FAR (float): the false alarm rate in [alarms/s]
- Returns:
- range (float): threshold to noise ratio
- Raises:
- No exception is raised.
-
pyradi.ryutils.detectSignalToNoiseThresholdToNoisePd(ThresholdToNoise, pD)¶ Solve for the signal to noise ratio, given the threshold to noise ratio and probability of detection.
Using the theory of matched filter design, calculate the signal to noise ratio, to achieve a required probability of detection.
References:
“Electro-optics handbook,” Tech. Rep. EOH-11, RCA, 1974. RCA Technical Series Publication.
- Hippenstiel, Detection Theory: Applications and Digital Signal Pro-cessing, CRC Press, 2002
- Args:
- ThresholdToNoise (float): the threshold to noise ratio [-]pD (float): the probability of detection [-]
- Returns:
- range (float): signal to noise ratio
- Raises:
- No exception is raised.
-
pyradi.ryutils.detectThresholdToNoiseSignalToNoisepD(SignalToNoise, pD)¶ Solve for the threshold to noise ratio, given the signal to noise ratio and probability of detection.
References:
“Electro-optics handbook,” Tech. Rep. EOH-11, RCA, 1974. RCA Technical Series Publication.
- Hippenstiel, Detection Theory: Applications and Digital Signal Pro-cessing, CRC Press, 2002
- Args:
- SignalToNoise (float): the signal to noise ratio [-]pD (float): the probability of detection [-]
- Returns:
- range (float): signal to noise ratio
- Raises:
- No exception is raised.
-
pyradi.ryutils.detectProbabilityThresholdToNoiseSignalToNoise(ThresholdToNoise, SignalToNoise)¶ - Solve for the probability of detection, given the signal to noise ratio and
- threshold to noise ratio
References:
“Electro-optics handbook,” Tech. Rep. EOH-11, RCA, 1974. RCA Technical Series Publication.
- Hippenstiel, Detection Theory: Applications and Digital Signal Pro-cessing, CRC Press, 2002
- Args:
- ThresholdToNoise (float): the threshold to noise ratio [-]SignalToNoise (float): the signal to noise ratio [-]
- Returns:
- range (float): probability of detection
- Raises:
- No exception is raised.
-
pyradi.ryutils.detectFARThresholdToNoisepulseWidth(ThresholdToNoise, pulseWidth)¶ Solve for the FAR, given the threshold to noise ratio and pulse width, for matched filter.
References:
“Electro-optics handbook,” Tech. Rep. EOH-11, RCA, 1974. RCA Technical Series Publication.
- Hippenstiel, Detection Theory: Applications and Digital Signal Pro-cessing, CRC Press, 2002
- Args:
- ThresholdToNoise (float): the threshold to noise ratio.pulseWidth (float): the signal pulse width in [s].
- Returns:
- FAR (float): the false alarm rate in [alarms/s]
- Raises:
- No exception is raised.
-
pyradi.ryutils.upMu(uprightMu=True, textcomp=False)¶ Returns a LaTeX micron symbol, either an upright version or the normal symbol.
The upright symbol requires that the siunitx LaTeX package be installed on the computer running the code. This function also changes the Matplotlib rcParams file.
- Args:
- uprightMu (bool): signals upright (True) or regular (False) symbol (optional).textcomp (bool): if True use the textcomp package, else use siunitx package (optional).
- Returns:
- range (string): LaTeX code for the micro symbol.
- Raises:
- No exception is raised.
-
pyradi.ryutils.cart2polar(x, y)¶ Converts from cartesian to polar coordinates, given (x,y) to (r,theta).
- Args:
- x (float np.array): x values in array format.y (float np.array): y values in array format.
- Returns:
- r (float np.array): radial component for given (x,y).theta (float np.array): angular component for given (x,y).
- Raises:
- No exception is raised.
original code by Joe Kington https://stackoverflow.com/questions/3798333/image-information-along-a-polar-coordinate-system
-
pyradi.ryutils.polar2cart(r, theta)¶ Converts from polar to cartesian coordinates, given (r,theta) to (x,y).
- Args:
- r (float np.array): radial values in array format.theta (float np.array): angular values in array format.
- Returns:
- x (float np.array): x component for given (r, theta).y (float np.array): y component for given (r, theta).
- Raises:
- No exception is raised.
original code by Joe Kington https://stackoverflow.com/questions/3798333/image-information-along-a-polar-coordinate-system
-
pyradi.ryutils.index_coords(data, origin=None, framesFirst=True)¶ Creates (x,y) zero-based coordinate arrrays for a numpy array indices, relative to some origin.
This function calculates two meshgrid arrays containing the coordinates of the input array. The origin of the new coordinate system defaults to the center of the image, unless the user supplies a new origin.
The data format can be data.shape = (rows, cols, frames) or data.shape = (frames, rows, cols), the format of which is indicated by the framesFirst parameter.
- Args:
- data (np.array): array for which coordinates must be calculated.origin ( (x-orig, y-orig) ): data-coordinates of where origin should beframesFirst (bool): True if data.shape is (frames, rows, cols), False if data.shape is (rows, cols, frames)
- Returns:
- x (float np.array): x coordinates in array format.y (float np.array): y coordinates in array format.
- Raises:
- No exception is raised.
original code by Joe Kington https://stackoverflow.com/questions/3798333/image-information-along-a-polar-coordinate-system
-
pyradi.ryutils.framesFirst(imageSequence)¶ Image sequence with frames along axis=2 (last index), reordered such that frames are along axis=0 (first index).
Image sequences are stored in three-dimensional arrays, in rows, columns and frames. Not all libraries share the same sequencing, some store frames along axis=0 and others store frames along axis=2. This function reorders an image sequence with frames along axis=2 to an image sequence with frames along axis=0. The function uses np.transpose(imageSequence, (2,0,1))
- Args:
- imageSequence (3-D np.array): image sequence in three-dimensional array, frames along axis=2
- Returns:
- ((3-D np.array): reordered three-dimensional array (view or copy)
- Raises:
- No exception is raised.
-
pyradi.ryutils.framesLast(imageSequence)¶ Image sequence with frames along axis=0 (first index), reordered such that frames are along axis=2 (last index).
Image sequences are stored in three-dimensional arrays, in rows, columns and frames. Not all libraries share the same sequencing, some store frames along axis=0 and others store frames along axis=2. This function reorders an image sequence with frames along axis=0 to an image sequence with frames along axis=2. The function uses np.transpose(imageSequence, (1,2,0))
- Args:
- imageSequence (3-D np.array): image sequence in three-dimensional array, frames along axis=0
- Returns:
- ((3-D np.array): reordered three-dimensional array (view or copy)
- Raises:
- No exception is raised.
-
pyradi.ryutils.rect(x, y, sx=1, sy=1)¶ Generation of a rectangular aperture.
- Args:
- x (np.array[N,M]): x-grid, metresy (np.array[N,M]): x-grid, metressx (float): full size along x.sy (float): full size along y.
- Returns:
- Nothing.
- Raises:
- No exception is raised.
Author: CJ Willers
Original source: http://arxiv.org/pdf/1412.4031.pdf
-
pyradi.ryutils.circ(x, y, d=1)¶ Generation of a circular aperture.
- Args:
- x (np.array[N,M]): x-grid, metresy (np.array[N,M]): y-grid, metresd (float): diameter in metres.comment (string): the symbol used to comment out lines, default value is None.delimiter (string): delimiter used to separate columns, default is whitespace.
- Returns:
- z (np.array[N,M]): z-grid, 1’s inside radius, meters/pixels.
- Raises:
- No exception is raised.
Author: Prof. Jason Schmidt, revised/ported by CJ Willers
Original source: http://arxiv.org/pdf/1412.4031.pdf
-
pyradi.ryutils.poissonarray(inp, seedval=None, tpoint=1000)¶ This routine calculates a Poisson random variable for an array of input values with potentially very high event counts.
At high mean values the Poisson distribution calculation overflows. For mean values exceeding 1000, the Poisson distribution may be approximated by a Gaussian distribution.
The function accepts a two-dimensional array and calculate a separate random value for each element in the array, using the element value as the mean value. A typical use case is when calculating shot noise for image data.
From http://en.wikipedia.org/wiki/Poisson_distribution#Related_distributions For sufficiently large values of
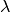 , (say
, (say 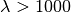 ),
the normal distribution with mean
),
the normal distribution with mean 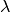 and
variance
and
variance 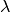 (standard deviation
(standard deviation 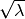 )
is an excellent approximation to the Poisson distribution.
If
)
is an excellent approximation to the Poisson distribution.
If 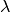 is greater than about 10, then the normal distribution
is a good approximation if an appropriate continuity correction is performed, i.e.,
is greater than about 10, then the normal distribution
is a good approximation if an appropriate continuity correction is performed, i.e.,
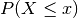 , where (lower-case) x is a non-negative integer, is replaced by
, where (lower-case) x is a non-negative integer, is replaced by
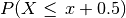 .
.
This function returns values of zero when the input is zero.
- Args:
- inp (np.array[N,M]): array with mean valueseedval (int): seed for random number generator, None means use system time.tpoint (int): Threshold when to switch over between Poisson and Normal distributions
- Returns:
- outp (np.array[N,M]): Poisson random variable for given mean value
- Raises:
- No exception is raised.
Author: CJ Willers
-
pyradi.ryutils.draw_siemens_star(outfile, n, dpi)¶ Siemens star chart generator
by Libor Wagner, http://cmp.felk.cvut.cz/~wagnelib/utils/star.html
- Args:
- outfile (str): output image filename (monochrome only)n (int): number of spokes in the output image.dpi (int): dpi in output image, determines output image size.
- Returns:
- Nothing, creates a monochrome siemens star image
- Raises:
- No exception is raised.
Author: Libor Wagner, adapted by CJ Willers
-
pyradi.ryutils.gen_siemens_star(origin, radius, n)¶
-
pyradi.ryutils.drawCheckerboard(rows, cols, numPixInBlock, imageMode, colour1, colour2, imageReturnType='image', datatype=<class 'numpy.uint8'>)¶ Draw checkerboard with 8-bit pixels
From http://stackoverflow.com/questions/2169478/how-to-make-a-checkerboard-in-numpy
- Args:
- rows (int) : number or rows in checkerboardcols (int) : number of columns in checkerboardnumPixInBlock (int) : number of pixels to be used in one block of the checkerboardimageMode (string) : PIL image mode [e.g. L (8-bit pixels, black and white), RGB (3x8-bit pixels, true color)]colour1 (int or RGB tuple) : colour 1 specified according to the imageModecolour2 (int or RGB tuple) : colour 2 specified according to the imageModeimageReturnType: ‘image’ for PIL image, ‘nparray’ for numpy arraydatatype (numpy data type) : numpy data type for the returned np.array
- Returns:
- img : checkerboard numpy array or PIL image (see imageReturnType)
- Raises:
- No exception is raised.
Example Usage:
rows = 5 cols = 7 pixInBlock = 4
color1 = 0 color2 = 255 img = drawCheckerboard(rows,cols,pixInBlock,’L’,color1,color2,’nparray’) pilImg = Img.fromarray(img, ‘L’) pilImg.save(‘{0}.png’.format(‘checkerboardL’))
color1 = (0,0,0) color2 = (255,255,255) pilImage = drawCheckerboard(rows,cols,pixInBlock,’RGB’,color1,color2,’image’) pilImage.save(‘{0}.png’.format(‘checkerboardRGB’))
-
pyradi.ryutils.makemotionsequence(imgfilename, mtnfilename, postfix, intTime, frmTim, outrows, outcols, imgRatio, pixsize, numsamples, fnPlotInput=None)¶ Builds a video from a still image and a displacement motion file.
The objective with this function is to create a video sequence from a still image, as if the camera moved minutely during the sensor integration time.
A static image is moved according to the (x,y) displacement motion in an input file. The input file must be at least ten times plus a bit larger than the required output file. The image input file is sampled with appropriate displacement for each point in the displacement file and pixel vlaues are accumulated in the output image. All of this temporal displacement and accumulation takes place in the context of a frame integration time and frame frequency.
The key requirements for accuracy in this method is an input image with much higher resolution than the output image, plus a temporal displacement file with much higher temporal sampling than the sensor integration time.
The function creates a sequence of images that can be used to create a video. Images are numbered in sequence, using the same base name as the input image. The sequence is generated in the current working directory.
The function currently processes only monochrome images (M,N) arrays.
The motion data file must be a compressed numpy npz or text file, with three columns: First column must be time, then movement along rows, then movement along columns. The units and scale of the motion columns must be the same units and scale as the pixel size in the output image.
imgRatio x imgRatio number of pixels in the input (hires) image are summed together and stored in one output image pixel. In other words if imgRatio is ten, each pixel in the output image will be the sum of 100 pixels in the imput image. During one integration time period the hires input image will be sampled at slightly different offsets (according to the motion file) and accumulated in an intermediate internal hires file. This intermediate internal file is collapsed as described above.
The function creates a series-numbered sequence if images that can be used to construct a video. One easy means to create the video is to use VirtualDub, available at www.virtualdub.org/index. In VirtualDub open the first image file in the numbered sequence, VirtualDub will then recognise the complete sequence as a video. Once loaded in VirtualDub, save the video as avi.
- Args:
- imgfilename (str): static image filename (monochrome only)mtnfilename (str): motion data filename.postfix (str): add this string to the end of the output filename.intTime (float): sensor integration time.frmTim (float): sensor frame time.outrows (int): number of rows in the output image.outcols (int): number of columns in the output image.imgRatio (float): hires image pixel count block size of one output image pixelpixsize (float): pixel size in same units as motion file.numsamples (int): number of motion input samples to be processed (-1 for all).fnPlotInput (str): output plot filename (None for no plot).
- Returns:
- True if successful, message otherwise, creates numbered images in current working directory
- Raises:
- No exception is raised.
Author: CJ Willers
-
pyradi.ryutils.extractGraph(filename, xmin, xmax, ymin, ymax, outfile=None, doPlot=False, xaxisLog=False, yaxisLog=False, step=None, value=None)¶ Scan an image containing graph lines and produce (x,y,value) data.
This function processes an image, calculate the location of pixels on a graph line, and then scale the (r,c) or (x,y) values of pixels with non-zero values. The
Get a bitmap of the graph (scan or screen capture). Take care to make the graph x and y axes horizontal/vertical. The current version of the software does not work with rotated images. Bitmap edit the graph. Clean the graph to the maximum extent possible, by removing all the clutter, such that only the line to be scanned is visible. Crop only the central block that contains the graph box, by deleting the x and y axes notation and other clutter. The size of the cropped image must cover the range in x and y values you want to cover in the scan. The graph image/box must be cut out such that the x and y axes min and max correspond exactly with the edges of the bitmap. You must end up with nothing in the image except the line you want to digitize.
The current version only handles single lines on the graph, but it does handle vertical and horizontal lines.
The function can also write out a value associated with the (x,y) coordinates of the graph, as the third column. Normally these would have all the same value if the line represents an iso value.
The x,y axes can be lin/lin, lin/log, log/lin or log/log, set the flags.
- Args:
- filename: name of the image filexmin: the value corresponding to the left side (column=0)xmax: the value corresponding to the right side (column=max)ymin: the value corresponding to the bottom side (row=bottom)ymax: the value corresponding to the top side (row=top)outfile: write the sampled points to this output filedoPlot: plot the digitised graph for visual validationxaxisLog: x-axis is in log10 scale (min max are log values)yaxisLog: y-axis is in log10 scale (min max are log values)step: if not None only ouput every step valuesvalue: if not None, write this value as the value column
- Returns:
- outA: a numpy array with columns (xval, yval, value)side effect: a file may be writtenside effect: a graph may be displayed
- Raises:
- No exception is raised.
Author: neliswillers@gmail.com
-
pyradi.ryutils.luminousEfficiency(vlamtype='photopic', wavelen=None, eqnapprox=False)¶ Returns the photopic luminous efficiency function on wavelength intervals
Type must be one of:
photopic: CIE Photopic V(lambda) modified by Judd (1951) and Vos (1978) [also known as CIE VM(lambda)] scotopic: CIE (1951) Scotopic V’(lambda) CIE2008v2: 2 degree CIE “physiologically-relevant” luminous efficiency Stockman & Sharpe CIE2008v10: 10 degree CIE “physiologically-relevant” luminous efficiency Stockman & Sharpe
For the equation approximations (only photoic and scotopic), if wavelength is not given a vector is created 0.3-0.8 um.
For the table data, if wavelength is not given a vector is read from the table.
CIE Photopic V(l) modified by Judd (1951) and Vos (1978) [also known as CIE VM(l)] from http://www.cvrl.org/index.htm
- Args:
- vlamtype (str): type of curve requiredwavelen (np.array[]): wavelength in umeqnapprox (bool): if False read tables, if True use equation
- Returns:
- luminousEfficiency (np.array[]): luminous efficiencywavelen (np.array[]): wavelength in um
- Raises:
- No exception is raised.
Author: CJ Willers
-
pyradi.ryutils.calcMTFwavefrontError(sample, wfdisplmnt, xg, yg, specdef, samplingStride=1, clear='Clear')¶ Given a mirror figure error, calculate MTF degradation from ideal
An aperture has an MTF determined by its shape. A clear aperture has zero phase delay and the MTF is determined only by the aperture shape. Any phase delay/error in the wavefront in the aperture will result in a lower MTF than the clear aperture diffraction MTF.
This function calculates the MTF degradation attributable to a wavefront error, relative to the ideal aperture MTF.
The optical transfer function is the Fourier transform of the point spread function, and the point spread function is the square absolute of the inverse Fourier transformed pupil function. The optical transfer function can also be calculated directly from the pupil function. From the convolution theorem it can be seen that the optical transfer function is the autocorrelation of the pupil function <https://en.wikipedia.org/wiki/Optical_transfer_function>.
The pupil function comprises a masking shape (the binary shape of the pupil) and a transmittance and spatial phase delay inside the mask. A perfect aperture has unity transmittance and zero phase delay in the mask. Some pupils have irregular pupil functions/shapes and hence the diffraction MTF has to be calculated numerically using images (masks) of the pupil function.
From the OSA Handbook of Optics, Vol II, p 32.4: For an incoherent optical system, the OTF is proportional to the two-dimensional autocorrelation of the exit pupil. This calculation can account for any phase factors across the pupil, such as those arising from aberrations or defocus. A change of variables is required for the identification of an autocorrelation (a function of position in the pupil) as a transfer function (a function of image-plane spatial frequency). The change of variables is
xi = {x}/{lambda d_i}
where $x$ is the autocorrelation shift distance in the pupil, $lambda$ is the wavelength, and $d_i$ is the distance from the exit pupil to the image. A system with an exit pupil of full width $D$ has an image-space cutoff frequency (at infinite conjugates) of
xi_{cutoff} ={D}/{lambda f}
In this analysis we assume that 1. the sensor is operating at infinite conjugates. 2. the mask falls in the entrance pupil shape.
The MTF is calculated as follows:
- Read in the pupil function mask and create an image of the mask.
- Calculate the two-dimensional autocorrelation function of the binary image (using the SciPy two-dimensional correlation function signal.correlate2d).
- Scale the magnitude and $(x,y)$ dimensions according to the dimensions of the physical pupil.
The the array containing the wavefront displacement in the pupil must have np.nan values outside the pupil. The np.nan values are ignored and not included in the calculation. Obscurations can be modelled by placing np.nan in the obscuration.
The specdef dictionary has a string key to identify (name) the band, with a single float contents which is the wavelength associated with this band.
- Args:
- sample (string): an identifier string to be used in the plotswfdisplmnt (nd.array[M,N]): wavefront displacement in mxg (nd.array[M,N]): x values from meshgrid, for wfdisplmntyg (nd.array[M,N]): y values from meshgrid, for wfdisplmntspecdef (dict): dictionary defining spectral wavelengthssamplingStride (number): sampling stride to limit size and processingclear (string): defines the dict key for clear aperture reference
- Returns:
- dictionaries below have entries for all keys in specdef.wfdev (dict): subsampled wavefront error in mphase (dict): subsampled wavefront error in radpupfn (dict): subsampled complex pupil functionMTF2D (dict): 2D MTF in (x,y) formatMTFpol (dict): 2D MTF in (r,theta) formatspecdef (): specdef dictionary as passed plus clear entryMTFmean (dict): mean MTF across all rotation anglesrho (nd.array[M,]): spatial frequency scale in cy/mradfcrit (float): cutoff or critical spatial frequency cy/mradclear (string): key used to signify the clear aperture case.
- Raises:
- No exception is raised.
-
pyradi.ryutils.intify_tuple(tup)¶ Make tuple entries int type